Simple Quadratic Formula Solver For The TI-84
Plus installation instructions
Super helpful tool, right on your calculator
The story
In my Junior year of highschool, I took precalculus. I clung on to that class with a D, but I did have a lot of fun discovering what the TI-84's were capable of.
I was importing Flappy Bird clones, Super Mario Bros, and Chess when I decided to make my own programs.
I started with making tools to format the graphing window better in TI's built in language. Then I discovered CE toolchain.
To be fair, I don't remember much about this project as it was quite a while ago, so I'll make this short-
I created my SQRT solver, and decided to expand it to fully solve the quadratic formula.
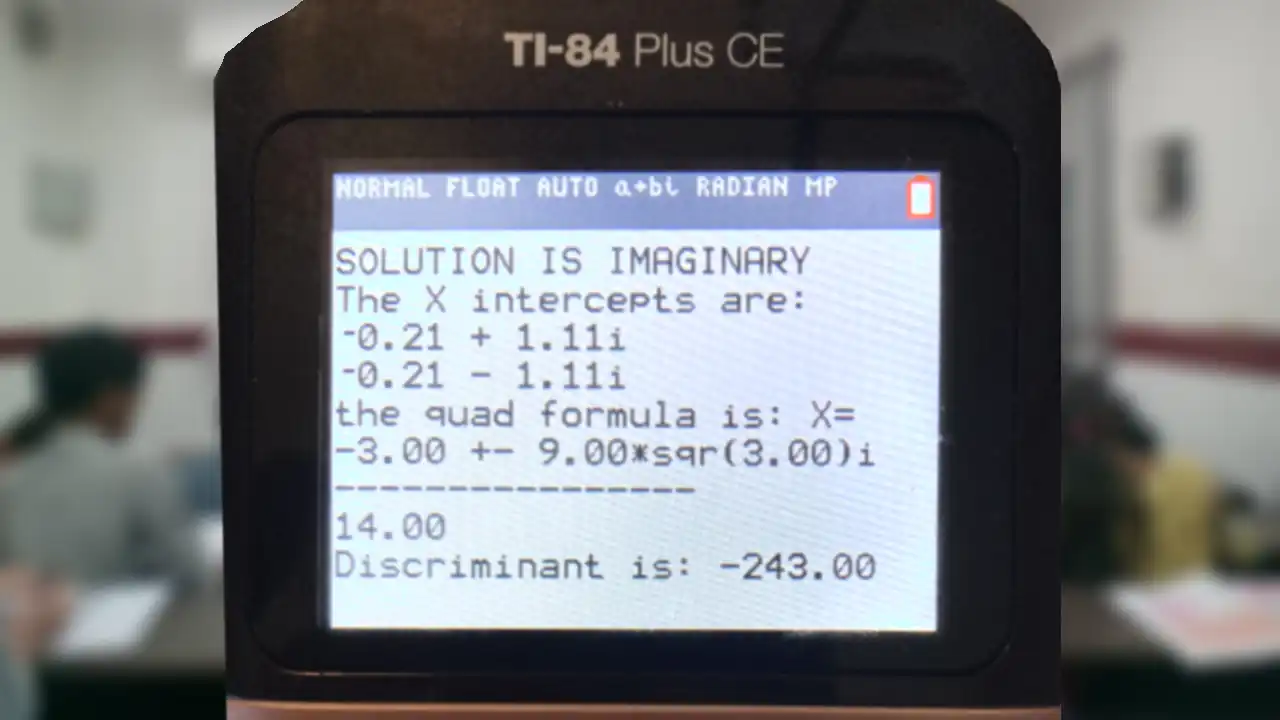
This means that when you give it the variables A, B, and C from the standard form, it will spit out a fully solved quadratic formula for you.
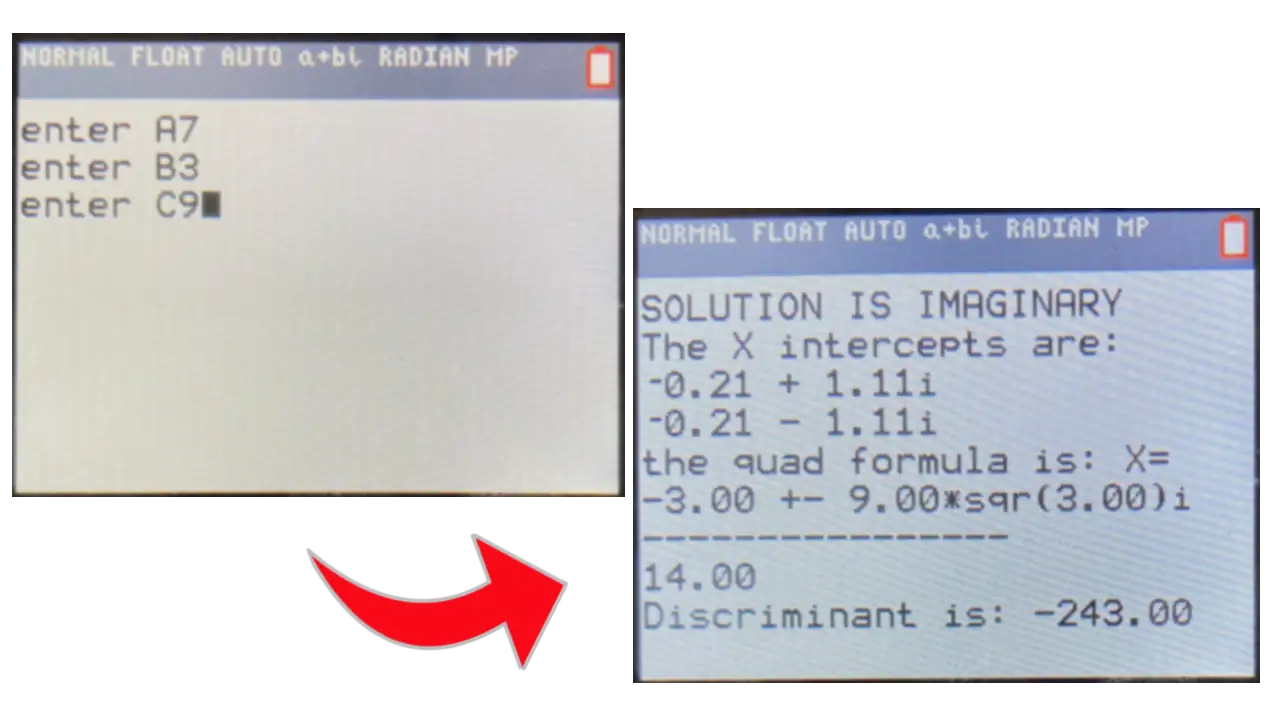
(It gives the decimal answers and the full thing with the roots and everything)
At the bottom of the page, I will describe how to get this working on your TI84 calculator quickly
Anyways, here's the 350 or so lines of code. Yeah, it's a little messy, but I tested it in like 95% of edge cases so it should work. There might be a weird input or two that you can give it to trip it up, but if that ever happens then I encourage you to tinker with the code a little!
The code
/*
*--------------------------------------
* Program Name: quadraticSolver
* Author: Aengus Patterson
* License: Mit License
* Description: Asks user for A,B,C input and solves for X in the quadradic formula
*--------------------------------------
*/
#include <ti/screen.h>
#include <ti/getcsc.h>
#include <ti/real.h>
#include <stdlib.h>
#include <math.h>
/*
---------------------FUNCTION DATA---------------------
Author: Aengus Patterson
Date: 10-20-2022
license: MIT license
Required Libs: <stdlib.h>
Input: square, where square is S in the formula below
Output: K, where K is in the formula below
Formula: sqrt(s) = sqrt(K) * sqrt(square/K)
Example: sqrt(24) = 2 * sqrt(6)
*/
//to find K, we go through every number up to square to see if it is
// 1) divisible by square
// 2) a perfect square
int simpSqrt(int square)
{
//the value of K may not change so we set it to 1
int K = 1;
for (int i = 2; i <= square; i++)
{
//if i is divisible by square, then we can move on
if (square % i == 0)
{
//the algorithm below is used so you don't have to include <math.h>
//its a square root algorithm that only gives the output (endNum) correctly when
//the input (i) is a perfect square, which is good because that's what we want.
int counter = 1, squareRoot = 1, endNum;
while (squareRoot <= i)
{
counter++;
squareRoot = counter * counter;
}
endNum = counter - 1;
//if the square of endNum == i, then it's a perfect square.
if (endNum * endNum == i)
{
//set K equal to i. This may be set multiple (or no) times throughout this loop.
K = i;
}
}
}
return K;
}
void float2str(float value, char *str)
{
real_t tmp_real = os_FloatToReal(value);
os_RealToStr(str, &tmp_real, 8, 1, 2);
}
int main(void)
{
//temporary string used for inputs
char tempStr[] = "0";
//A in the quadratic formula
float a = 0;
//B in the quadratic formula
float b = 0;
//C in the quadracic formula
float c = 0;
//d is the discriminant of the quadratic forumula
float d = 0;
//the 3 greatest common factors for optimizations and whatnot.
int gcfOfBAnd2A = 1;
int gcfOfBAndK = 1;
int gcfOfAll = 1;
//used to determine whether or not to add in "i"
bool negativeDiscriminant = false;
//used to determing whether or not to perform gcd optimization
bool allIntegers = true;
//used to determine whether or not to find K in the simplified sqrt formula
bool integerDiscriminant = true;
//this is just used to store the string when converting
char buffer[10] = {'\0'};
//clear the home
os_ClrHome();
//gather a,b,c inputs and convert them to ints
os_GetStringInput("enter A", tempStr, 512);
a = atof(tempStr);
os_NewLine();
os_GetStringInput("enter B", tempStr, 512);
b = atof(tempStr);
os_NewLine();
os_GetStringInput("enter C", tempStr, 512);
c = atof(tempStr);
os_ClrHome();
d = (b*b) - (4*a*c);
if (d < 0)
{
negativeDiscriminant = true;
d *= -1;
os_PutStrFull("SOLUTION IS IMAGINARY");
os_NewLine();
}
//find and print the values of the two different x possibilities
os_PutStrFull("The X intercepts are: ");
os_NewLine();
if (!negativeDiscriminant)
{
float x1 = (-b + (sqrt(d))) / (2 * a);
float2str(x1, buffer);
os_PutStrFull(buffer);
}
else
{
float2str(-b / (2 * a), buffer);
os_PutStrFull(buffer);
os_PutStrFull(" + ");
float2str(sqrt(d) / (2 * a), buffer);
os_PutStrFull(buffer);
os_PutStrFull("i");
}
os_NewLine();
if (!negativeDiscriminant)
{
float x2 = (-b - (sqrt(d))) / (2 * a);
float2str(x2, buffer);
os_PutStrFull(buffer);
}
else
{
float2str(-b / (2 * a), buffer);
os_PutStrFull(buffer);
os_PutStrFull(" - ");
float2str(sqrt(d) / (2 * a), buffer);
os_PutStrFull(buffer);
os_PutStrFull("i");
}
//the following checks for least common factor optimizations
//after finding the gcf of 2a and b, and b and sqrt of k, then we find the gcf of those two and use that to factor out of everything.
int n1 = 1;
int n2 = 1;
int integerD = (int)d;
int integerA = (int)a;
int integerB = (int)b;
int integerC = (int)c;
if (integerA == a && integerB == b && integerC == c)
{
allIntegers = true;
}
if (integerD != d)
{
integerDiscriminant = false;
}
else if (allIntegers)
{
n1 = b;
n2 = 2 * a;
n1 = ( n1 > 0) ? n1 : -n1;
n2 = ( n2 > 0) ? n2 : -n2;
while(n1!=n2)
{
if(n1 > n2)
n1 -= n2;
else
n2 -= n1;
}
gcfOfBAnd2A = n1;
n1 = b;
n2 = sqrt(simpSqrt(d));
n1 = ( n1 > 0) ? n1 : -n1;
n2 = ( n2 > 0) ? n2 : -n2;
while(n1!=n2)
{
if(n1 > n2)
n1 -= n2;
else
n2 -= n1;
}
gcfOfBAndK = n1;
n1 = gcfOfBAnd2A;
n2 = gcfOfBAndK;
n1 = ( n1 > 0) ? n1 : -n1;
n2 = ( n2 > 0) ? n2 : -n2;
while(n1!=n2)
{
if(n1 > n2)
n1 -= n2;
else
n2 -= n1;
}
gcfOfAll = n1;
}
//prints the quadratic formula, with actual variables subbed in.
os_NewLine();
os_PutStrFull("the quad formula is: X=");
os_NewLine();
if (b > 0)
{
//if b is negative, then it cancels out on the quad form thing.
os_PutStrFull("-");
}
if (d!= 0)
{
float2str(b / gcfOfAll, buffer);
}
else
{
float2str(b / gcfOfBAnd2A, buffer);
}
os_PutStrFull(buffer);
//code in this if statemnet prints off the +- sqrt(b^2 -4ac) unless d is just 0
if (d != 0)
{
os_PutStrFull(" +- ");
if (integerDiscriminant)
{
float k = simpSqrt(d);
if ((int)(sqrt(k) / gcfOfAll) != 1)
{
float2str(sqrt(k) / gcfOfAll, buffer);
os_PutStrFull(buffer);
os_PutStrFull("*");
}
if (d!= 1)
{
os_PutStrFull("sqr(");
float2str(d / k, buffer);
os_PutStrFull(buffer);
os_PutStrFull(")");
}
else
{
os_PutStrFull("1");
}
if (negativeDiscriminant)
{
os_PutStrFull("i");
}
}
else
{
if (d!= 1)
{
os_PutStrFull("sqr(");
float2str(d, buffer);
os_PutStrFull(buffer);
os_PutStrFull(")");
}
else
{
os_PutStrFull("1");
}
if (negativeDiscriminant)
{
os_PutStrFull("i");
}
}
}
if (!((d!= 0 && 2 * a / gcfOfAll == 1) || (d== 0 && 2 * a/ gcfOfBAnd2A == 1)))
{
os_NewLine();
os_PutStrFull("----------------");
os_NewLine();
if (d != 0)
{
float2str(2 * a / gcfOfAll, buffer);
}
else
{
float2str(2 * a/ gcfOfBAnd2A, buffer);
}
os_PutStrFull(buffer);
}
os_NewLine();
os_PutStrFull("Discriminant is: ");
if (negativeDiscriminant)
{
os_PutStrFull("-");
}
float2str(d, buffer);
os_PutStrFull(buffer);
while (!os_GetCSC());
return 0;
}
Install Instructions
First, download Artifice. It's just a terminal that allows you to run this type of application by using some software exploits.
Next, download this file. It's all of the aforementioned code compiled using the Toolchain.
Import both of those files onto your calculator using the TI Connect app. You can send them to RAM or Archive, but RAM is more volotile and is prone to resets.
Turn on your calculator, and go to Apps. Select CabriJr.
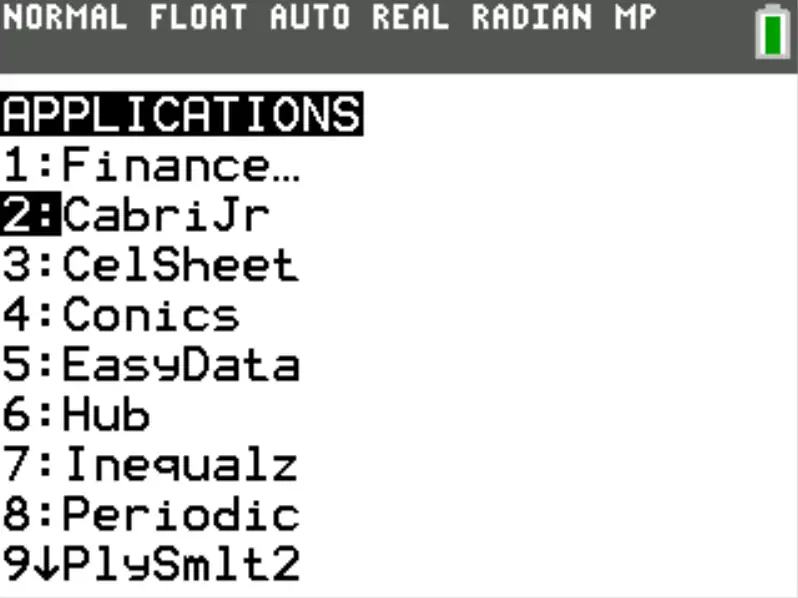
CabriJr is an app used to launch other apps. Weird, huh?
Now we need to run Artifice. If the menu doesn't pop up, hit Y= . Then go down to open, and hit Artifice.
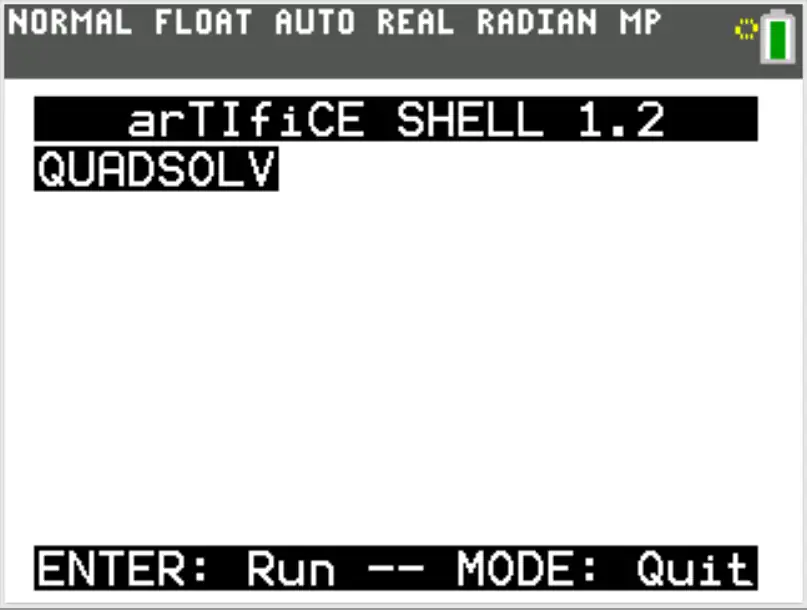
Now we are in the Artifice terminal and able to launch our program.
Launch the program and start tinkering around with it!

If you're looking to streamline the app execution process a little more, you can look into getting Cesium .
I hope you were able to learn something from this tutorial, and maybe bump your grade up a little bit :)